Core Advantage
核心优势

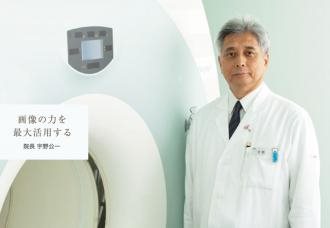
中国西南领先
优可利成立于2014年,总部位于成都,是中国西南地区领先的跨境医疗服务提供商,“倾听,探究,托付”是我们对客户的承诺和宗旨。

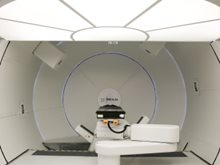
美国排名前十的医疗机构
优可利只与美国排名前十的医疗机构签署协议并进行深度合作,能准确、快速地为您预约顶尖医疗专家并提供相关医疗服务。

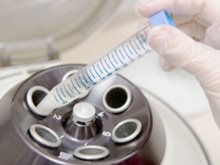
试管婴儿“0”服务费
作为美国顶尖试管婴儿中心在中国西南地区唯一的授权代理机构,我们承诺,不向客户收取任何中间费用,做到“0”服务费,所有费用由客户直接与海外医疗机构对接,支付。让客户安心放心,全程无忧。

全程一对一陪同
优可利将为您提供一对一全程陪同及翻译服务,细心协助您与医疗机构之间的沟通,同时为您及家属精心安排海外的吃、住、行等各项生活配套服务,让您的海外医旅生活轻松便捷,安心康复。

尊享荣誉
优可利成立以来,与顶尖海外机构深度合作,并取得了对方的认可和授权。目前,优可利在海外医疗、海外试管婴儿、海外精密体检三个领域中都与相关机构达成协议,共同搭建海外医疗平台。

最高可享医疗费用50%减免
我们根据客户的具体情况,将他们转诊到最适合自己病情的医疗机构,尽量为他们降低治疗成本,将费用降到可承传范围。解决他们在国内医院无法解决的难题,最高还可获得医疗费用50%减免。
关于我们 ABOUT US
达州市皮肤性病防治中心于2004年08月19日成立。法定代表人陈国成,公司经营范围包括:外科皮肤科;皮肤病专业;性传播疾病专业医学检验科中医科)等。医院(Hospital)一词来自拉丁文,原意为“客人”,因为一开始设立时,是供人避难,还备有休息间,使来者舒适,有招待意图,后来,才逐渐成为满足人类医疗需求,提供医疗服务的专业机构,收容和治疗病人的服务场所。医院是指按照法律法规和行业规范,为病员开展必要的医学检查、治疗措施、护理技术、接诊服务、康复设备、救治运输等服务,以救死扶伤为主要目的的医疗机构,其服务对象不仅包括有症状的病员和伤员,也包括不能自理或活动受限有医疗护理依赖的老年人,法医评定有医...
NEWS CENTER
新闻资讯
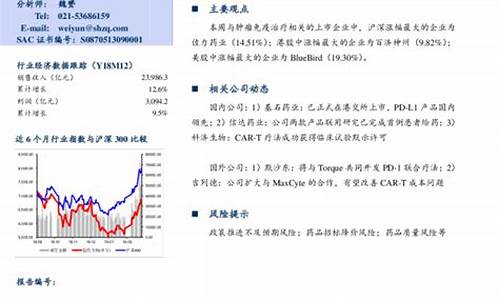
在全球范围内,生物医药领域的发展日新月异,新药的研发与上市一直是业内外关注的热点。随着科技的进步和临床需求的增加,越来越多的新药成功突破研发阶段,为广大患者带来希望。本文将详细介绍近期一个引人注目的新药上市动态,从其研发背景到临床试验,再到最终的市场表现,提供一个全面的视角。
研发背景与动机新药的研发往往源于对某一疾病深入的理解和长期的科研积累。本次上市的···
15
2025-01
研发背景与动机新药的研发往往源于对某一疾病深入的理解和长期的科研积累。本次上市的新药主要针对罕见疾病,研发团队通过多年的基础研究,确定了疾病的分子机制,从而开
14
2025-01
视频中强调了定期口腔检查的重要性。青少年应该每年至少进行一次口腔检查,及时发现和治疗口腔疾病。视频介绍了正确的刷牙方法和使用牙线的重要性。正确的刷牙方
12
2025-01
一、上皮组织上皮组织是口腔最常见的组织类型,包括口腔黏膜、唾液腺、颊粘膜等。在病理学上,上皮组织的病变可以分为良性和恶性两种类型。常见的良性上皮病变包括炎症、溃疡、疣、息
30
2024-12
1. 每天刷牙两次每天至少刷牙两次,每次2-3分钟,使用牙线和漱口水来清洁牙齿和口腔。这可以帮助去除食物残渣和细菌,并减少龋齿和牙周病的风险。1. 定期看牙医每年至少看一次牙医